9.1 向量值函数在有向曲线上的积分
向量场
若场中每一点对应的物理量是向量,则称该场为向量场。
若场中每一点对应的物理量是数量,则称该场为数量场。
若 $G$ 是一平面向量场,则可以用一个定义在 $G$ 上的二元向量值函数表示:
\symbfit{\overrightarrow{F}}(x,y)=P(x,y)\symbfit{\overrightarrow{i}}+Q(x,y)\symbfit{\overrightarrow{j}}
$$
若 $G$ 是一空间向量场,则可以用一个定义在 $G$ 上的三元向量值函数表示:
\symbfit{\overrightarrow{A}}(x,y,z)=P(x,y,z)\symbfit{\overrightarrow{i}}+Q(x,y,z)\symbfit{\overrightarrow{j}}+R(x,y,z)\symbfit{\overrightarrow{k}}
$$
向量线是位于向量场中这样的曲线:该曲线上每一点处的切线与该点的场向量重合。
向量场中的曲线有方向的概念。沿不同的方向积累的数值是相反的。我们规定非封闭曲线 $L$ 的两个端点 $A$ $B$ 有两个方向 $\stackrel\frown{AB}$ $\stackrel\frown{BA}$ 中的一个方向记为 $L$ 。另一个为 $L^-$ .
第二型曲线积分
定义:
设 $L$ 是空间中从点 $A$ 到点 $B$ 的一条有向光滑曲线段, $\symbfit{\overrightarrow{e_r}}$ 为 $L$ 上任一点 $(x,y,z)$ 处的单位切向量,其方向与 $L$ 的方向一致。在 $L$ 上定义一个向量值函数$\symbfit{\overrightarrow{A}}(x,y,z)=P(x,y,z)\symbfit{\overrightarrow{i}}+Q(x,y,z)\symbfit{\overrightarrow{j}}+R(x,y,z)\symbfit{\overrightarrow{k}}$ , 其中 $P(x,y,z),Q(x,y,z),R(x,y,z)$ 在 $L$ 上有界,若数量积 $\symbfit{\overrightarrow{A}} \cdot \symbfit{\overrightarrow{e_r}}$ 在 $L$ 上的第一型曲线积分存在,则称此积分值为向量值函数 $\symbfit{\overrightarrow{A}}$ 在有向曲线段 $L$ 上的积分,或称第二型曲线积分。
\int_L\symbfit{\overrightarrow{A}}\,\cdot\,\symbfit{\overrightarrow{e_r}}\,\mathrm{d}s
$$
在直角坐标系中,记 $\symbfit{\overrightarrow{e_r}}=(\cos\alpha,\cos\beta,\cos\gamma)$ , 则有 $\symbfit{\overrightarrow{e_r}}\,\mathrm{d}s=(\mathrm{d}x,\mathrm{d}y,\mathrm{d}z)$ , 这时称 $\symbfit{\overrightarrow{e_r}}\,\mathrm{d}s$ 为有向弧微分,简写为 $\mathrm{d}\symbfit{\overrightarrow{s}}$ .
此时第二型曲线积分式子可以表示为:
\int_L\symbfit{\overrightarrow{A}}\,\cdot\,\mathrm{d}\symbfit{\overrightarrow{s}}=\int_LP(x,y,z)\mathrm{d}x+Q(x,y,z)\mathrm{d}y+R(x,y,z)\mathrm{d}z
$$
简记为
\int_L\symbfit{\overrightarrow{A}}\,\cdot\,\mathrm{d}\symbfit{\overrightarrow{s}}=\int_LP\mathrm{d}x+Q\mathrm{d}y+R\mathrm{d}z
$$
称为第二型曲线积分的坐标形式,因此也称第二型曲线积分为对坐标的曲线积分。
第二型曲线积分有线性性,可加性,有向性,都比较直观容易想象。
第二型曲线积分的计算
设空间有向光滑曲线段 $L$ 的参数方程为
\left\{\begin{array}{l}
x=x(t),
\\
y=y(t),
\\
z=z(t) \hfill
\end{array}\right.
\ \ (t:\alpha \to\beta)
$$
则有第二型曲线计算公式:
\int_LP\mathrm{d}x+Q\mathrm{d}y+R\mathrm{d}z=\int_\alpha^\beta\bigg[\,P(t)\,x'(t)+Q(t)\,y'(t)+R(t)\,z'(t)\,\bigg]\mathrm{d}t
$$
9.2 Green公式、平面曲线积分与路径无关的条件
平面区域有关概念
设 $D$ 为平面区域,如果 $D$ 内任意一条闭曲线所围部分都属于 $D$ ,则称 $D$为单连通区域;否则称 $D$ 为复连通区域.
直观上说,单连通区域不能有 “洞” .

平面区域 $D$ 有其边界曲线 $L$ , 规定 $L$ 的正向为:沿着正向行走时,区域 $D$ 总是在左边。即单连通区域的边界曲线 $L$ 的正向为逆时针方向,复连通区域的外边界曲线正向也是逆时针方向,而内边界曲线的正向为顺时针方向。
本节所讨论的闭曲线都是简单闭曲线,除了两个端点重合外,曲线自身不相交。
复联通区域可以通过划分转换为多个单连通区域。
格林公式
设平面闭区域 $D$ 是由分段光滑的闭曲线 $L$ 围成的单连通区域,函数 $P(x,y),Q(x,y)$ 上具有一阶连续偏导数,则有格林公式
{\int \kern{-20mu} \bigcirc}_L\, P\, \mathrm{d}x +Q\,\mathrm{d}y=\iint_D\Big(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial x}\Big)\, \mathrm{d}x\mathrm{d}y.
$$
由格林公式可以计算平面闭区域 $D$ 的面积:
S=\iint_D\mathrm{d}x\mathrm{d}y=\frac{1}{2}{\int \kern{-20mu} \bigcirc}_L\Big(-y \,\mathrm{d}x+ x \,\mathrm{d}y\Big).
$$
积分与路径无关的条件
设 $D$ 为平面上的单连通区域,函数 $P(x,y),Q(x,y)$ 上具有一阶连续偏导数,则下列四个命题等价:
- 对于 $D$ 内任何分段光滑的闭曲线 $L$ ,有
{\int \kern{-20mu} \bigcirc}_L\, P\, \mathrm{d}x +Q\,\mathrm{d}y=0
$$
- 曲线积分 $\displaystyle{\int \kern{-20mu} \bigcirc}_L\, P\, \mathrm{d}x +Q\,\mathrm{d}y$ 的值在 $D$ 内与路径无关。
- 表达式 $P\, \mathrm{d}x +Q\,\mathrm{d}y$在 $D$ 内是某个二元函数 $u=(x,y)$ 的全微分,即
\mathrm{d}u(x,y)=P\, \mathrm{d}x +Q\,\mathrm{d}y
$$
- 等式在 $D$ 内处处成立.
\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}
$$
此定理非常重要,它指出了平面上第二型曲线积分与路径无关的充要条件,也指出了表达式 $P\mathrm{d}x+Q\mathrm{d}y$ 是某个二元函数的全微分的充要条件.在这些充要条件中,命题 (4) 在使用中最为方便.
当曲线积分与路径无关时,对于较复杂的曲线积分,可以换一条便于计算的路径来计算.
原函数、全微分方程
根据前面的定理,若函数 $P(x,y),Q(x,y)$ 在单连通区域 $D$ 上具有一阶连续偏导数,且在 $D$ 内满足 $\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}$ ,那么表达式 $P\, \mathrm{d}x +Q\,\mathrm{d}y$在 $D$ 内是某个二元函数 $u=(x,y)$ 的全微分,此时称 $u(x,y)$ 为 $P\, \mathrm{d}x +Q\,\mathrm{d}y$ 的一个原函数。$u(x,y)$ 可以由下面公式求得:
u(x,y)=\int_{(x_0,y_0)}^{(x,y)} P\,\mathrm{d}x+Q\,\mathrm{d}y
$$
这一过程被称为全微分求积。
因为此时积分与路径无关,因此可以选择简单的路径来计算积分,比如平直折线:
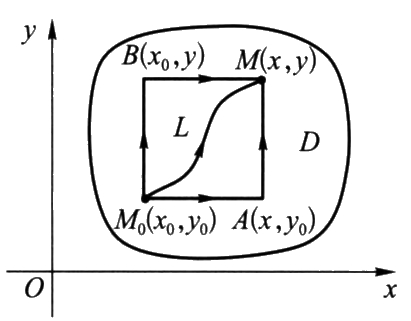
u(x,y)=\int_{x_0}^x P(x,y_0)\,\mathrm{d}x+\int_{y_0}^y Q(x,y)\,\mathrm{d}y
\\
\\
u(x,y)=\int_{y_0}^y Q(x_0,y)\,\mathrm{d}y+\int_{x_0}^x P(x,y)\,\mathrm{d}x
$$
如果一阶微分方程改写成
P(x,y)\,\mathrm{d}x+Q(x,y)\,\mathrm{d}y=0
$$
后,其左端恰好满足上述等价关系,则这个方程为全微分方程。此时 $u(x,y)=C$ 是隐式通解,其中 $C$ 是任意常数。
总结平面第二类曲线积分
给出一个第二类曲线积分,如何求解?
第一步:判断函数整体是否满足
\frac{\partial Q}{\partial x}\ {= \kern{-17mu} ^?}\ \frac{\partial P}{\partial y}
$$
如果不相等,则用 Green公式 或 直接设参数求定积分。
如果相等:
第二步:判断 $L$ 是否封闭
如果封闭,则利用积分与路径无关原则,重新选择路径计算
如果不封闭:
第三步:判断 $L$ 内部是否含有奇点(不满足第一公式)
如果没有奇点,直接 $=0$ .
如果有奇点,则只能用 Green公式(挖去奇点,加辅助线) 或 设参数求定积分。
9.3 第二型曲面积分
定义:
设 $S$ 是空间中一有向光滑曲面, $\symbfit{\overrightarrow{n_0}}$ 为 $S$ 上任一点 $M(x,y,z)$ 处的单位法向量,其方向与 $S$ 的指定侧一致。在 $S$ 上定义一个向量值函数$\symbfit{\overrightarrow{A}}(x,y,z)=P(x,y,z)\symbfit{\overrightarrow{i}}+Q(x,y,z)\symbfit{\overrightarrow{j}}+R(x,y,z)\symbfit{\overrightarrow{k}}$ , 其中 $P(x,y,z),Q(x,y,z),R(x,y,z)$ 在 $S$ 上有界,若数量积 $\symbfit{\overrightarrow{A}} \cdot \symbfit{\overrightarrow{n_0}}$ 在 $S$ 上的第一型曲面积分存在,则称此积分值为向量值函数 $\symbfit{\overrightarrow{A}}$ 在有向曲曲线 $S$ 上的积分,或称第二型曲面积分。
\iint_L\symbfit{\overrightarrow{A}}\,\cdot\,\symbfit{\overrightarrow{n_0}}\,\mathrm{d}S
$$
在直角坐标系中,记 $\symbfit{\overrightarrow{n_0}}=(\cos\alpha,\cos\beta,\cos\gamma)$ , 则有 $\symbfit{\overrightarrow{n_0}}\,\mathrm{d}S=(\mathrm{d}y\mathrm{d}z,\mathrm{d}z\mathrm{d}x,\mathrm{d}x\mathrm{d}y)$ , 这时称 $\symbfit{\overrightarrow{n_0}}\,\mathrm{d}S$ 为有向面积微元,简写为 $\mathrm{d}\symbfit{\overrightarrow{S}}$ .
此时第二型曲面积分式子可以表示为:
\iint_L\symbfit{\overrightarrow{A}}\,\cdot\,\mathrm{d}\symbfit{\overrightarrow{S}}=\iint_LP(x,y,z)\mathrm{d}y\mathrm{d}z+Q(x,y,z)\mathrm{d}z\mathrm{d}x+R(x,y,z)\mathrm{d}x\mathrm{d}y
$$
简记为
\int_L\symbfit{\overrightarrow{A}}\,\cdot\,\mathrm{d}\symbfit{\overrightarrow{s}}=\int_LP\mathrm{d}y\mathrm{d}z+Q\mathrm{d}z\mathrm{d}x+R\mathrm{d}x\mathrm{d}y
$$
称为第二型曲面积分的坐标形式,因此也称第二型曲面积分为对坐标的曲面积分。
第二型曲面积分有线性性,可加性,有向性,都比较直观容易想象。
第二型曲面积分的计算
设空间有向光滑曲线段 $S$ 的方程为
z=z(x,y)
$$
则有第二型曲线计算公式:
\iint_L\symbfit{\overrightarrow{A}}\,\cdot\,\symbfit{\overrightarrow{n_0}}\,\mathrm{d}S=\pm\iint\limits_{D_{xy}}\symbfit{\overrightarrow{A}}\big(x,y,z(x,y)\big)\,\cdot\symbfit{\overrightarrow{n}}\,\mathrm{d}x\mathrm{d}y
$$
其中 $\symbfit{\overrightarrow{n}}$ 取 $(-z_x,-z_y,1).$ $D_{xy}$ 是 $S$ 在 $Oxy$ 平面上的投影区域 . 当 $S$ 取上侧时为 $+$ ,取下侧时为 $-$ .
对于 $x=x(y,z)$ ,取右侧为 $+$ ;对于 $y=y(x,z)$ ,取前侧为 $+$ .
简便算法:设有向曲面 $S$ 的方程为 $z=z(x,y)$ , $S$ 在 $Oxy$ 平面上的投影区域为 $D_{xy}$ ,函数 $R(x,y,z)$ 在 $S$ 上连续,则有
\iint\limits_{S}R(x,y,z)\,\mathrm{d}x\mathrm{d}y=\pm \iint\limits_{D_{xy}}R\big(\,x,y,z(x,y)\,\big)\,\mathrm{d}x\mathrm{d}y
$$
当 $S$ 取上侧时为 $+$ , 当 $S$ 取下侧时为 $-$ .
\iint\limits_{S}P(x,y,z)\,\mathrm{d}y\mathrm{d}z=\pm \iint\limits_{D_{yz}}P\big(\,x(y,z),y,z\,\big)\,\mathrm{d}y\mathrm{d}z
$$
当 $S$ 取前侧时为 $+$ , 当 $S$ 取后侧时为 $-$ .
\iint\limits_{S}Q(x,y,z)\,\mathrm{d}z\mathrm{d}x=\pm \iint\limits_{D_{zx}}Q\big(\,x,y(z,x),z\,\big)\,\mathrm{d}z\mathrm{d}x
$$
当 $S$ 取右侧时为 $+$ , 当 $S$ 取左侧时为 $-$ .




Comments 2 条评论
伊雷娜!
伊蕾娜我真的好喜欢你啊