第九章向量值函数的曲线积分与曲面积分

9.1 向量值函数在有向曲线上的积分

向量场

若场中每一点对应的物理量是向量，则称该场为向量场。

若场中每一点对应的物理量是数量，则称该场为数量场。

若 $G$ 是一平面向量场，则可以用一个定义在 $G$ 上的二元向量值函数表示：

\vec{F} (x, y) = P (x, y) \vec{i} + Q (x, y) \vec{j}

若 $G$ 是一空间向量场，则可以用一个定义在 $G$ 上的三元向量值函数表示：

\vec{A} (x, y, z) = P (x, y, z) \vec{i} + Q (x, y, z) \vec{j} + R (x, y, z) \vec{k}

向量线是位于向量场中这样的曲线：该曲线上每一点处的切线与该点的场向量重合。

向量场中的曲线有方向的概念。沿不同的方向积累的数值是相反的。我们规定非封闭曲线 $L$ 的两个端点 $A$ $B$ 有两个方向 $\overset{⌢}{A B}$ $\overset{⌢}{B A}$ 中的一个方向记为 $L$ 。另一个为 $L^{-}$ .

第二型曲线积分

定义：

设 $L$ 是空间中从点 $A$ 到点 $B$ 的一条有向光滑曲线段， $\vec{e_{r}}$ 为 $L$ 上任一点 $(x, y, z)$ 处的单位切向量，其方向与 $L$ 的方向一致。在 $L$ 上定义一个向量值函数 $\vec{A} (x, y, z) = P (x, y, z) \vec{i} + Q (x, y, z) \vec{j} + R (x, y, z) \vec{k}$ , 其中 $P (x, y, z), Q (x, y, z), R (x, y, z)$ 在 $L$ 上有界，若数量积 $\vec{A} \cdot \vec{e_{r}}$ 在 $L$ 上的第一型曲线积分存在，则称此积分值为向量值函数 $\vec{A}$ 在有向曲线段 $L$ 上的积分，或称第二型曲线积分。

\int_{L} \vec{A} \cdot \vec{e_{r}} d s

在直角坐标系中，记 $\vec{e_{r}} = (\cos α, \cos β, \cos γ)$ , 则有 $\vec{e_{r}} d s = (d x, d y, d z)$ , 这时称 $\vec{e_{r}} d s$ 为有向弧微分，简写为 $d \vec{s}$ .

此时第二型曲线积分式子可以表示为：

\int_{L} \vec{A} \cdot d \vec{s} = \int_{L} P (x, y, z) d x + Q (x, y, z) d y + R (x, y, z) d z

简记为

\int_{L} \vec{A} \cdot d \vec{s} = \int_{L} P d x + Q d y + R d z

称为第二型曲线积分的坐标形式，因此也称第二型曲线积分为对坐标的曲线积分。

第二型曲线积分有线性性，可加性，有向性，都比较直观容易想象。

第二型曲线积分的计算

设空间有向光滑曲线段 $L$ 的参数方程为

{\begin{cases} x = x (t), \\ y = y (t), \\ z = z (t) \end{cases} (t : α \to β)

则有第二型曲线计算公式：

\int_{L} P d x + Q d y + R d z = \int_{α}^{β} [P (t) x^{'} (t) + Q (t) y^{'} (t) + R (t) z^{'} (t)] d t

9.2 Green公式、平面曲线积分与路径无关的条件

平面区域有关概念

设 $D$ 为平面区域，如果 $D$ 内任意一条闭曲线所围部分都属于 $D$ ，则称 $D$ 为单连通区域；否则称 $D$ 为复连通区域．

直观上说，单连通区域不能有 “洞” .

平面区域 $D$ 有其边界曲线 $L$ , 规定 $L$ 的正向为：沿着正向行走时，区域 $D$ 总是在左边。即单连通区域的边界曲线 $L$ 的正向为逆时针方向，复连通区域的外边界曲线正向也是逆时针方向，而内边界曲线的正向为顺时针方向。

本节所讨论的闭曲线都是简单闭曲线，除了两个端点重合外，曲线自身不相交。

复联通区域可以通过划分转换为多个单连通区域。

格林公式

设平面闭区域 $D$ 是由分段光滑的闭曲线 $L$ 围成的单连通区域，函数 $P (x, y), Q (x, y)$ 上具有一阶连续偏导数，则有格林公式

{\int ◯}_{L} P d x + Q d y = \iint_{D} (\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial x}) d x d y .

由格林公式可以计算平面闭区域 $D$ 的面积：

S = \iint_{D} d x d y = \frac{1}{2} {\int ◯}_{L} (- y d x + x d y) .

积分与路径无关的条件

设 $D$ 为平面上的单连通区域，函数 $P (x, y), Q (x, y)$ 上具有一阶连续偏导数，则下列四个命题等价：

对于 $D$ 内任何分段光滑的闭曲线 $L$ ，有

{\int ◯}_{L} P d x + Q d y = 0

曲线积分 ${\int ◯}_{L} P d x + Q d y$ 的值在 $D$ 内与路径无关。
表达式 $P d x + Q d y$ 在 $D$ 内是某个二元函数 $u = (x, y)$ 的全微分，即

d u (x, y) = P d x + Q d y

等式在 $D$ 内处处成立.

\frac{\partial Q}{\partial x} = \frac{\partial P}{\partial y}

此定理非常重要，它指出了平面上第二型曲线积分与路径无关的充要条件，也指出了表达式 $P d x + Q d y$ 是某个二元函数的全微分的充要条件．在这些充要条件中，命题 (4) 在使用中最为方便．

当曲线积分与路径无关时，对于较复杂的曲线积分，可以换一条便于计算的路径来计算．

原函数、全微分方程

根据前面的定理，若函数 $P (x, y), Q (x, y)$ 在单连通区域 $D$ 上具有一阶连续偏导数，且在 $D$ 内满足 $\frac{\partial Q}{\partial x} = \frac{\partial P}{\partial y}$ ，那么表达式 $P d x + Q d y$ 在 $D$ 内是某个二元函数 $u = (x, y)$ 的全微分，此时称 $u (x, y)$ 为 $P d x + Q d y$ 的一个原函数。 $u (x, y)$ 可以由下面公式求得：

u (x, y) = \int_{(x_{0}, y_{0})}^{(x, y)} P d x + Q d y

这一过程被称为全微分求积。

因为此时积分与路径无关，因此可以选择简单的路径来计算积分，比如平直折线：

u (x, y) = \int_{x_{0}}^{x} P (x, y_{0}) d x + \int_{y_{0}}^{y} Q (x, y) d y u (x, y) = \int_{y_{0}}^{y} Q (x_{0}, y) d y + \int_{x_{0}}^{x} P (x, y) d x

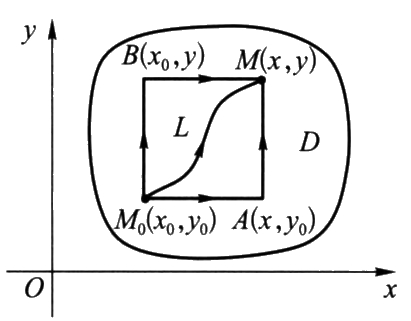
如果一阶微分方程改写成

P (x, y) d x + Q (x, y) d y = 0

后，其左端恰好满足上述等价关系，则这个方程为全微分方程。此时 $u (x, y) = C$ 是隐式通解，其中 $C$ 是任意常数。

总结平面第二类曲线积分

给出一个第二类曲线积分，如何求解？

第一步：判断函数整体是否满足

\frac{\partial Q}{\partial x} =^{?} \frac{\partial P}{\partial y}

如果不相等，则用 Green公式或直接设参数求定积分。

如果相等：

第二步：判断 $L$ 是否封闭

如果封闭，则利用积分与路径无关原则，重新选择路径计算

如果不封闭：

第三步：判断 $L$ 内部是否含有奇点（不满足第一公式）

如果没有奇点，直接 $= 0$ .

如果有奇点，则只能用 Green公式（挖去奇点，加辅助线）或设参数求定积分。

9.3 第二型曲面积分

定义：

设 $S$ 是空间中一有向光滑曲面， $\vec{n_{0}}$ 为 $S$ 上任一点 $M (x, y, z)$ 处的单位法向量，其方向与 $S$ 的指定侧一致。在 $S$ 上定义一个向量值函数 $\vec{A} (x, y, z) = P (x, y, z) \vec{i} + Q (x, y, z) \vec{j} + R (x, y, z) \vec{k}$ , 其中 $P (x, y, z), Q (x, y, z), R (x, y, z)$ 在 $S$ 上有界，若数量积 $\vec{A} \cdot \vec{n_{0}}$ 在 $S$ 上的第一型曲面积分存在，则称此积分值为向量值函数 $\vec{A}$ 在有向曲曲线 $S$ 上的积分，或称第二型曲面积分。

\iint_{L} \vec{A} \cdot \vec{n_{0}} d S

在直角坐标系中，记 $\vec{n_{0}} = (\cos α, \cos β, \cos γ)$ , 则有 $\vec{n_{0}} d S = (d y d z, d z d x, d x d y)$ , 这时称 $\vec{n_{0}} d S$ 为有向面积微元，简写为 $d \vec{S}$ .

此时第二型曲面积分式子可以表示为：

\iint_{L} \vec{A} \cdot d \vec{S} = \iint_{L} P (x, y, z) d y d z + Q (x, y, z) d z d x + R (x, y, z) d x d y

简记为

\int_{L} \vec{A} \cdot d \vec{s} = \int_{L} P d y d z + Q d z d x + R d x d y

称为第二型曲面积分的坐标形式，因此也称第二型曲面积分为对坐标的曲面积分。

第二型曲面积分有线性性，可加性，有向性，都比较直观容易想象。

第二型曲面积分的计算

设空间有向光滑曲线段 $S$ 的方程为

z = z (x, y)

则有第二型曲线计算公式：

\iint_{L} \vec{A} \cdot \vec{n_{0}} d S = \pm \iint_{D_{x y}} \vec{A} (x, y, z (x, y)) \cdot \vec{n} d x d y

其中 $\vec{n}$ 取 $(- z_{x}, - z_{y}, 1) .$ $D_{x y}$ 是 $S$ 在 $O x y$ 平面上的投影区域 . 当 $S$ 取上侧时为 $+$ ，取下侧时为 $-$ .

对于 $x = x (y, z)$ ，取右侧为 $+$ ；对于 $y = y (x, z)$ ,取前侧为 $+$ .

简便算法：设有向曲面 $S$ 的方程为 $z = z (x, y)$ , $S$ 在 $O x y$ 平面上的投影区域为 $D_{x y}$ ，函数 $R (x, y, z)$ 在 $S$ 上连续，则有

\iint_{S} R (x, y, z) d x d y = \pm \iint_{D_{x y}} R (x, y, z (x, y)) d x d y

当 $S$ 取上侧时为 $+$ , 当 $S$ 取下侧时为 $-$ .

\iint_{S} P (x, y, z) d y d z = \pm \iint_{D_{y z}} P (x (y, z), y, z) d y d z

当 $S$ 取前侧时为 $+$ , 当 $S$ 取后侧时为 $-$ .

\iint_{S} Q (x, y, z) d z d x = \pm \iint_{D_{z x}} Q (x, y (z, x), z) d z d x

当 $S$ 取右侧时为 $+$ , 当 $S$ 取左侧时为 $-$ .

回溯点

第九章向量值函数的曲线积分与曲面积分

9.1 向量值函数在有向曲线上的积分