$\S 8.1 $ 二重积分的概念与性质
二重积分的概念
概念略
定理 8.1 (可积的必要条件) 若函数 $f(x,y)$ 在有界闭区域 $D$ 上可积,则 $f(x,y)$ 在 $D$ 上有界。
定理 8.2 (可积的充分条件) 若 $f(x,y)$ 是有界闭区域 $D$ 上的连续函数,则 $f(x,y)$ 在 $D$ 上可积。
$\S 8.2$ 二重积分的计算
直角坐标系下二重积分的计算
\begin{gather}
x\text{ 型域下}\displaystyle\iint\limits_{D}f(x,y)d\sigma=\displaystyle\int_a^b\mathrm{d}x\displaystyle\int_{\varphi_1(x)}^{\varphi_2(x)}f(x,y)\mathrm{d}y
\\
y\text{ 型域下}\displaystyle\iint\limits_{D}f(x,y)d\sigma=\displaystyle\int_c^d\mathrm{d}y\displaystyle\int_{\psi_1(y)}^{\psi_2(y)}f(x,y)\mathrm{d}x
\end{gather}
$$
 |  |
极坐标系下二重积分的计算
极坐标变换:
\left\{\begin{matrix}
x=r\cos\theta \hfill
\\
y=r\sin\theta \hfill
\\
D \to D_{r\theta} \hfill
\end{matrix}\right.
$$
二重积分转换为:
\displaystyle\iint\limits_{D}f(x,y)d\sigma=\displaystyle{\iint\limits_{D_{r\theta}}}f(r\cos\theta,r\sin\theta)\cdot r\,\mathrm{d}r\,\mathrm{d}\theta=\displaystyle\int_\alpha^\beta \mathrm{d}\theta\displaystyle\int_{r_1(\theta)}^{r_2(\theta)}f(r\cos\theta,r\sin\theta)r\,\mathrm{d}r
$$
一般的,当积分域 $D$ 是圆域或圆域的一部分(如版圆盘、扇形、圆环域等),且被积函数 $f(x,y)$ 有 $g(x^2+y^2)$ 或 $g(\frac{y}{x})$ 的形式时,用极坐标系计算二重积分是比较合适的。
二重积分的换元法
换元(其实也是一种坐标变换):
\left\{\begin{matrix}
x=x(u,v) \hfill
\\
y=y(u,v) \hfill
\\
D\to D_{uv} \hfill
\end{matrix}\right.
$$
还需满足:
- $x(u,v),y(u,v)$ 在 $D_{uv}$ 上具有一阶连续偏导数;
- 在 $D_{uv}$ 上 $\mathrm{Jacobi}$ 行列式$$
J=\frac{\partial(x,y)}{\partial(u,v)}=
\begin{vmatrix}
{x}'_u & {x}'_v \\
{y}'_u & {y}'_v
\end{vmatrix}
\ne 0,\ \ (u,v) \in D_{uv},
$$
则有二重积分的换元公式
\displaystyle\iint\limits_{D}f(x,y)d\sigma=\displaystyle{\iint\limits_{D_{uv}}}f\big(\,x(u,v),y(u,v)\,\big)\cdot |J|\,\mathrm{d}u\,\mathrm{d}v
$$
例如,极坐标系变换就是一种换元。 $J=r$.
还需要记住的有广义极坐标变换:
\left\{\begin{matrix}
x=ar\cos\theta \hfill
\\
y=br\sin\theta \hfill
\\
D\to D_{r\theta} \hfill
\\
J=abr \hfill
\end{matrix}\right.
$$
二重积分的几何意义
有关二重积分的几何意义,将统一放到8.8里讲述。
$\S 8.3$ 三重积分
直角坐标系下的三重积分计算
坐标面投影法
xy\text{ 型域下}\iiint\limits_{V}f(x,y,z)\mathrm{d}V=\iint\limits_{D_{xy}}\mathrm{d}x\mathrm{d}y\int_{z_1(x,y)}^{z_2(x,y)}f(x,y,z)\mathrm{d}z.
$$
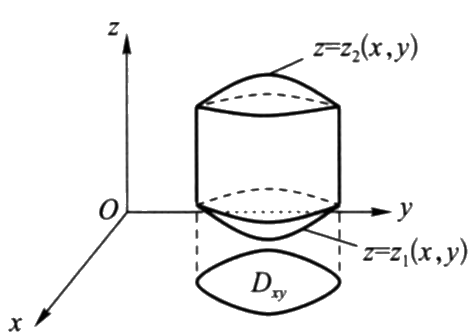
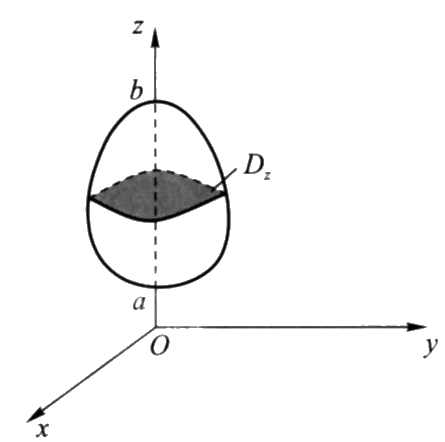
先二后一法
适用条件:某一轴平行截取物体的上下部分。
\iiint\limits_{V}f(x,y,z)\mathrm{d}V=\int_a^b \mathrm{d}z\iint\limits_{D_z}f(x,y,z)\mathrm{d}x\mathrm{d}y.
$$
三重积分的换元法
换元:
\left\{\begin{matrix}
x=x(u,v,w) \hfill
\\
y=y(u,v,w) \hfill
\\
z=z(u,v,w) \hfill
\\
D\to D_{uvw} \hfill
\\
J\not\equiv0 \hfill
\\
\text{换元后的函数一阶偏导连续} \hfill
\end{matrix}\right.
$$
则有三重积分的换元计算公式
\displaystyle\iiint\limits_{V}f(x,y,z)dV=\displaystyle{\iiint\limits_{D_{uvw}}}f\big(\,x(u,v,w),y(u,v,w),z(u,v,w)\,\big)\cdot |J|\,\mathrm{d}u\,\mathrm{d}v\,\mathrm{d}w
$$
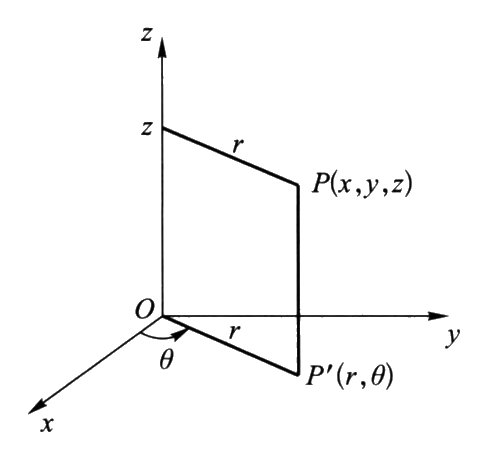
柱面坐标系下三重积分的计算
点 $P$ 的直角坐标与柱面坐标的关系为
\left\{\begin{matrix}
x=r\cos\theta \hfill
\\
y=r\sin\theta \hfill
\\
z=z \hfill
\\
J=r \hfill
\end{matrix}\right.
$$
三重积分在柱面坐标系下的变换公式为
\iiint\limits_{V}f(x,y,z)dV={\iiint\limits_{D_{r\theta z}}}f\big(\,r\cos\theta,r\sin\theta,z\,\big)\cdot r\,\mathrm{d}r\,\mathrm{d}\theta\,\mathrm{d}z
$$
一般而言,当被积函数具有 $g=(x^2+y^2,z)$ 的形式,而积分域 $V$ 是以 $z$ 轴为旋转轴的旋转体或旋转体的一部分时,利用柱面坐标计算三重积分比较简单。
球面坐标系下三重积分的计算
点 $P$ 的直角坐标与球面坐标的关系为
\left\{\begin{matrix}
x=\rho\sin\varphi\cos\theta \hfill
\\
y=\rho\sin\varphi\sin\theta \hfill
\\
z=\rho\cos\varphi \hfill
\\
J=\rho^2\sin\varphi \hfill
\end{matrix}\right.
$$
三重积分在柱面坐标系下的变换公式为
\iiint\limits_{V}f(x,y,z)dV={\iiint\limits_{D_{\rho\varphi\theta}}}f\big(\,\rho\sin\varphi\cos\theta,\rho\sin\varphi\sin\theta,\rho\cos\varphi\,\big)\cdot \rho^2\sin\varphi\,\mathrm{d}\rho\,\mathrm{d}\varphi\,\mathrm{d}\theta
$$
一般而言,当被积函数具有 $g=(x^2+y^2+z^2)$ 的形式,而积分域 $V$ 为球体或球体的一部分(如半球、球壳等)时,利用球面坐标计算三重积分比较简单。

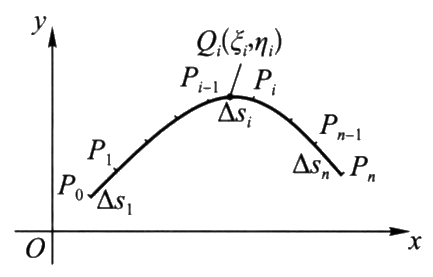
$\S 8.4$ 第一型曲线积分
第一型曲线积分的计算
若空间曲线 $L$ 的参数方程为
\left\{\begin{matrix}
x=x(t) \hfill
\\
y=y(t) \hfill
\\
z=z(t) \hfill
\end{matrix}\right.
\ \ (\alpha \le t \le \beta)
$$
当 $x(t),y(t),z(t)$ 在 [$\alpha,\beta$] 上具有一阶连续导数,且 $x'^2(t)+y'^2(t)+z'^2(t)\not\equiv 0$ ,函数 $f(x,y,z)$ 在 $L$ 上连续,则曲线积分 $\displaystyle\int_L f(x,y,z)\mathrm{d}s$ 存在,且
\displaystyle\int_L f(x,y,z)\mathrm{d}s=\displaystyle\int_\alpha^\beta f\big(\,x(t),y(t),z(t)\,\big)\sqrt{x'^2(t)+y'^2(t)+z'^2(t)}\ \mathrm{d}t
$$
$\S 8.5$ 第一型曲面积分
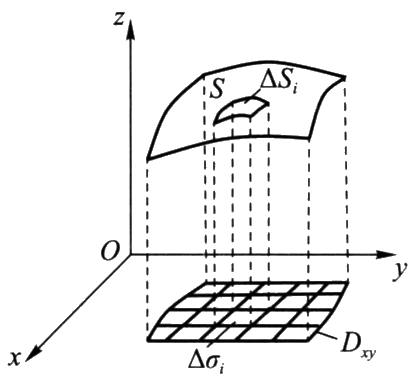
第一型曲面积分的计算
设曲面 $S$ 的方程为
z=z(x,y)\,,\ \ (x,y)\in D_{xy}
$$
则
\iint\limits_{S}f(x,y,z)\mathrm{d}S=\iint\limits_{D_{xy}}f\big(\,x,y,z(x,y)\,\big)\sqrt{1+z_x^2(x,y)+z_y^2(x,y)}\,\mathrm{d}x\,\mathrm{d}y
$$
$\S 8.6$ 几何与物理应用举例
二重积分的几何意义
二重积分 $\displaystyle\iint\limits_{D}f(x,y)d\sigma$ 的几何意义是:积分域 $D$ 上的平面薄板,其面密度为 $f(x,y)$ ,则二重积分为该平面薄板的质量。当 $f(x,y)=1$ 时,二重积分数值上即为积分域 $D$ 的面积。
另一个几何意义是:对于一个曲顶柱体,其 $xOy$ 平面的投影是有界闭区域 $D$ ,顶部满足方程 $f(x,y)$ ,则二重积分为该曲顶柱体的体积。

曲面的面积(第一型曲面积分的特殊情况)
利用二重积分不仅可以计算立体的体积和平面图形的面积,也可以计算曲面的面积。
对于一个曲面 $S$
z=z(x,y)\,,\ \ (x,y)\in D_{xy}
$$
证明过程略,直接给出求曲面面积的二重积分公式:
S=\iint\limits_{D_{xy}}\sqrt{1+z^2_x(x,y)+z^2_y(x,y)}\,\mathrm{d}x\,\mathrm{d}y
$$
对于 $x=x(y,z),\,\,y=y(x,z)$ 的形式同理,不再列出。
事实上,这就是第一型曲面积分在被积函数为 1 时的情况。

三重积分的几何意义
三重积分 $\displaystyle\iiint\limits_{V}f(x,y,z)dV$ 的几何意义是:积分域 $V$ 上的块状物体,其体密度为 $f(x,y,z)$ ,则三重积分为该物体的质量。当被积函数 $f(x,y,z)=1$ 时,三重积分数值上即为积分域 $V$ 的体积。
第一型曲线积分的几何意义
第一型曲线积分 $\displaystyle\int_{L}f(x,y)ds$ 的几何意义是:光滑曲线 $L$ 在点 $(x,y)$ 处的质量线密度为 $f(x,y)$ ,则第一型曲线积分为该曲线的质量。当被积函数为 $f(x,y)=1$ 时,第一型曲线积分数值上等于曲线的长度。
另一个几何意义是:对于一个柱面 $S$ ,它的母线平行于 $z$ 轴,准纤维 $xOy$ 平面上的曲线段 $L$ 。柱面的高度为 $f(x,y)$ ,则第一型曲线积分为该柱面的面积。

第一型曲面积分的几何意义
第一型曲线积分 $\displaystyle\iint\limits_{S}f(x,y,z)dS$ 的几何意义是:光滑曲面 $S$ 在点 $(x,y,z)$ 处的质量面密度为 $f(x,y,z)$ ,则第一型曲面积分为该曲面的质量。当被积函数 $f(x,y,z)=1$ 时,第一型曲面积分数值上等于曲面的面积。
静矩
什么是静矩?对于一个质点 $(x,y,z)$ ,则称 $M_{xy}=m \cdot z$ 为该质点对 $xOy$ 坐标面的静矩。
那么对一个物体 $V$ ,其体密度函数为 $\rho(x,y,z)$ ,则整个物体对 $xOy,yOz,xOz$ 坐标面的静矩分别为
\begin{gather}
M_{xy}=\iiint\limits_{V}z\cdot\rho(x,y,z)\,\mathrm{d}V
\\
M_{yz}=\iiint\limits_{V}x\cdot\rho(x,y,z)\,\mathrm{d}V
\\
M_{xz}=\iiint\limits_{V}y\cdot\rho(x,y,z)\,\mathrm{d}V
\\
\end{gather}
$$
对一个平面薄板 $S$ ,其面密度函数为 $\rho(x,y)$ ,则整个物体对 $x,y$ 轴的静矩分别为
\begin{gather}
M_x=\iint\limits_{D}y\cdot\rho(x,y)\,\mathrm{d}\sigma
\\
M_y=\iint\limits_{D}x\cdot\rho(x,y)\,\mathrm{d}\sigma
\end{gather}
$$
质心
对一个物体 $V$ ,其体密度函数为 $\rho(x,y,z)$ ,则该物体的质心坐标计算公式为:
\begin{gather}
{\overline{x}}=\frac{M_{yz}}{m}=\frac{\displaystyle\iiint\limits_{V}x\cdot\rho(x,y,z)\,\mathrm{d}V}{\displaystyle\iiint\limits_{V}\rho(x,y,z)\,\mathrm{d}V}
\\
\\
{\overline{y}}=\frac{M_{xz}}{m}=\frac{\displaystyle\iiint\limits_{V}y\cdot\rho(x,y,z)\,\mathrm{d}V}{\displaystyle\iiint\limits_{V}\rho(x,y,z)\,\mathrm{d}V}
\\
\\
{\overline{z}}=\frac{M_{xy}}{m}=\frac{\displaystyle\iiint\limits_{V}z\cdot\rho(x,y,z)\,\mathrm{d}V}{\displaystyle\iiint\limits_{V}\rho(x,y,z)\,\mathrm{d}V}
\\
\\
\end{gather}
$$
对一个平面薄板 $S$ ,其面密度函数为 $\rho(x,y)$ ,则该平板状物体的质心坐标计算公式为:
\begin{gather}
{\overline{x}}=\frac{M_{y}}{m}=\frac{\displaystyle\iint\limits_{D}x\cdot\rho(x,y)\,\mathrm{d}\sigma}{\displaystyle\iint\limits_{D}\rho(x,y)\,\mathrm{d}\sigma}
\\
\\
{\overline{y}}=\frac{M_{x}}{m}=\frac{\displaystyle\iint\limits_{D}y\cdot\rho(x,y)\,\mathrm{d}\sigma}{\displaystyle\iint\limits_{D}\rho(x,y)\,\mathrm{d}\sigma}
\\\\
\end{gather}
$$
转动惯量
力学上称 $I_l=m \cdot r^2$ 为该质点对定轴 $l$ 的转动惯量。
对一个物体 $V$ ,其体密度函数为 $\rho(x,y,z)$ ,则该物体的对 $x,y,z$ 轴的转动惯量分别为:
\begin{gather}
I_x=\displaystyle\iiint\limits_{V}(y^2+z^2)\cdot\rho(x,y,z)\,\mathrm{d}V
\\\\
I_y=\displaystyle\iiint\limits_{V}(x^2+z^2)\cdot\rho(x,y,z)\,\mathrm{d}V
\\\\
I_z=\displaystyle\iiint\limits_{V}(x^2+y^2)\cdot\rho(x,y,z)\,\mathrm{d}V
\\\\
\end{gather}
$$
对一个平面薄板 $D$ ,其面密度函数为 $\rho(x,y)$ ,则该平板状物体对 $x,y$ 轴的转动惯量分别为:
\begin{gather}
I_x=\displaystyle\iint\limits_{D}y^2\cdot\rho(x,y)\,\mathrm{d}\sigma
\\\\
I_y=\displaystyle\iint\limits_{D}x^2\cdot\rho(x,y)\,\mathrm{d}\sigma
\end{gather}
$$
引力
万有引力公式 $F=G\frac{m_1\cdot m_2}{r^2}$,
一个物体 $V$ 对质点 $(x_0,y_0,z_0)$ 的引力 $F=(F_x,F_y,F_z)$ ,设物体上某一点为 $(x,y,z)$ ,两点之间的距离为 $r=\sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2}$,则有公式:
\begin{gather}
F_x=\iiint\limits_{V} F_x=\iiint\limits_{V} G\frac{m_0\,\rho(x,y,z)\,(x-x_0)}{r^3}\, \mathrm{d}V
\\
F_y=\iiint\limits_{V} F_y=\iiint\limits_{V} G\frac{m_0\,\rho(x,y,z)\,(y-y_0)}{r^3}\, \mathrm{d}V
\\
F_z=\iiint\limits_{V} F_z=\iiint\limits_{V} G\frac{m_0\,\rho(x,y,z)\,(z-z_0)}{r^3}\, \mathrm{d}V
\\
\end{gather}
$$




Comments NOTHING